【单位圆里 Dot & Det】

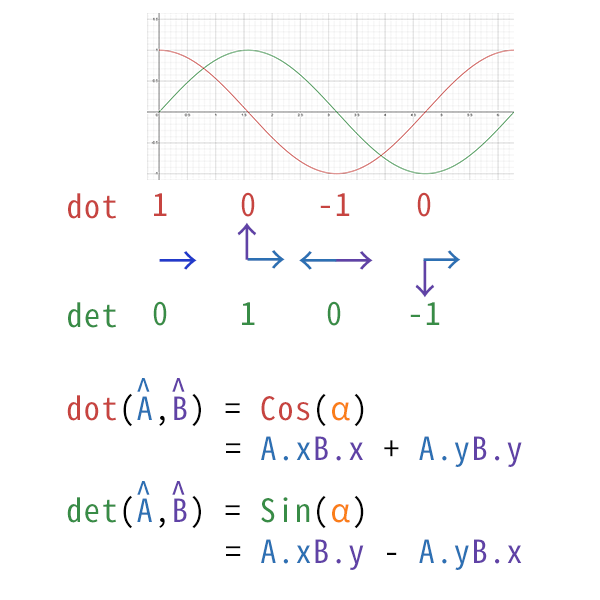
Dot 全称 dot product

Det 全称 determinant

dot

向量点乘,求两个向量夹角的阴影长度,值在 -1 ~ 1 之间

• 本质是cos函数。
• 垂直时值为0。
• 方向同向时，值为1。
• 方向相反时，值为-1。
• 具有交换律，互换向量后结果不变。
• 用于判断两个向量的接近程度十分有用。

要求出α，则使用 acos(dot(a,b))

/** 计算两个向量构成夹角的弧度值 */
function radiansBetweenVectors(vector1, vector2) 
{
    // 计算向量的点积
    const dotProduct = vector1[0] * vector2[0] + vector1[1] * vector2[1];

    // 计算向量的长度
    const magnitude1 = Math.sqrt(vector1[0] * vector1[0] + vector1[1] * vector1[1]);
    const magnitude2 = Math.sqrt(vector2[0] * vector2[0] + vector2[1] * vector2[1]);

    // 计算夹角的余弦值
    const cosine = dotProduct / (magnitude1 * magnitude2);

    // 计算夹角的弧度值
    const angleInRadians = Math.acos(cosine);

    return angleInRadians;
}

det

2D 版的叉乘,可以用于判断两个向量的左右关系

• 本质是sin函数。
• 同向或者反向时，值为0。
• 不同方向时，值的正负不一样。
• 没有交换律，互换向量后结果相反。