【3D矩阵】

很多意义都与2d矩阵一致，只是比2d矩阵多一个z轴。

内存里数据结构如图所示：

创建Matrix4x4

public Matrix4x4(Vector4 column0, Vector4 column1, Vector4 column2, Vector4 column3)
{
    this.m00 = column0.x; this.m01 = column1.x; this.m02 = column2.x; this.m03 = column3.x;
    this.m10 = column0.y; this.m11 = column1.y; this.m12 = column2.y; this.m13 = column3.y;
    this.m20 = column0.z; this.m21 = column1.z; this.m22 = column2.z; this.m23 = column3.z;
    this.m30 = column0.w; this.m31 = column1.w; this.m32 = column2.w; this.m33 = column3.w;
}

传参参考下图：

Matrix4x4 相乘

这个操作可以进行多个矩阵的合并。

public static Matrix4x4 operator*(Matrix4x4 lhs, Matrix4x4 rhs)
{
    Matrix4x4 res;
    res.m00 = lhs.m00 * rhs.m00 + lhs.m01 * rhs.m10 + lhs.m02 * rhs.m20 + lhs.m03 * rhs.m30;
    res.m01 = lhs.m00 * rhs.m01 + lhs.m01 * rhs.m11 + lhs.m02 * rhs.m21 + lhs.m03 * rhs.m31;
    res.m02 = lhs.m00 * rhs.m02 + lhs.m01 * rhs.m12 + lhs.m02 * rhs.m22 + lhs.m03 * rhs.m32;
    res.m03 = lhs.m00 * rhs.m03 + lhs.m01 * rhs.m13 + lhs.m02 * rhs.m23 + lhs.m03 * rhs.m33;

    res.m10 = lhs.m10 * rhs.m00 + lhs.m11 * rhs.m10 + lhs.m12 * rhs.m20 + lhs.m13 * rhs.m30;
    res.m11 = lhs.m10 * rhs.m01 + lhs.m11 * rhs.m11 + lhs.m12 * rhs.m21 + lhs.m13 * rhs.m31;
    res.m12 = lhs.m10 * rhs.m02 + lhs.m11 * rhs.m12 + lhs.m12 * rhs.m22 + lhs.m13 * rhs.m32;
    res.m13 = lhs.m10 * rhs.m03 + lhs.m11 * rhs.m13 + lhs.m12 * rhs.m23 + lhs.m13 * rhs.m33;

    res.m20 = lhs.m20 * rhs.m00 + lhs.m21 * rhs.m10 + lhs.m22 * rhs.m20 + lhs.m23 * rhs.m30;
    res.m21 = lhs.m20 * rhs.m01 + lhs.m21 * rhs.m11 + lhs.m22 * rhs.m21 + lhs.m23 * rhs.m31;
    res.m22 = lhs.m20 * rhs.m02 + lhs.m21 * rhs.m12 + lhs.m22 * rhs.m22 + lhs.m23 * rhs.m32;
    res.m23 = lhs.m20 * rhs.m03 + lhs.m21 * rhs.m13 + lhs.m22 * rhs.m23 + lhs.m23 * rhs.m33;

    res.m30 = lhs.m30 * rhs.m00 + lhs.m31 * rhs.m10 + lhs.m32 * rhs.m20 + lhs.m33 * rhs.m30;
    res.m31 = lhs.m30 * rhs.m01 + lhs.m31 * rhs.m11 + lhs.m32 * rhs.m21 + lhs.m33 * rhs.m31;
    res.m32 = lhs.m30 * rhs.m02 + lhs.m31 * rhs.m12 + lhs.m32 * rhs.m22 + lhs.m33 * rhs.m32;
    res.m33 = lhs.m30 * rhs.m03 + lhs.m31 * rhs.m13 + lhs.m32 * rhs.m23 + lhs.m33 * rhs.m33;

    return res;
}

Vector4 进行 Matrix4x4 变换

对一个Vector4进行矩阵变换操作。

public static Vector4 operator*(Matrix4x4 lhs, Vector4 vector)
{
    Vector4 res;
    res.x = lhs.m00 * vector.x + lhs.m01 * vector.y + lhs.m02 * vector.z + lhs.m03 * vector.w;
    res.y = lhs.m10 * vector.x + lhs.m11 * vector.y + lhs.m12 * vector.z + lhs.m13 * vector.w;
    res.z = lhs.m20 * vector.x + lhs.m21 * vector.y + lhs.m22 * vector.z + lhs.m23 * vector.w;
    res.w = lhs.m30 * vector.x + lhs.m31 * vector.y + lhs.m32 * vector.z + lhs.m33 * vector.w;
    return res;
}

缩放和平移如图所示：

旋转矩阵如图所示：

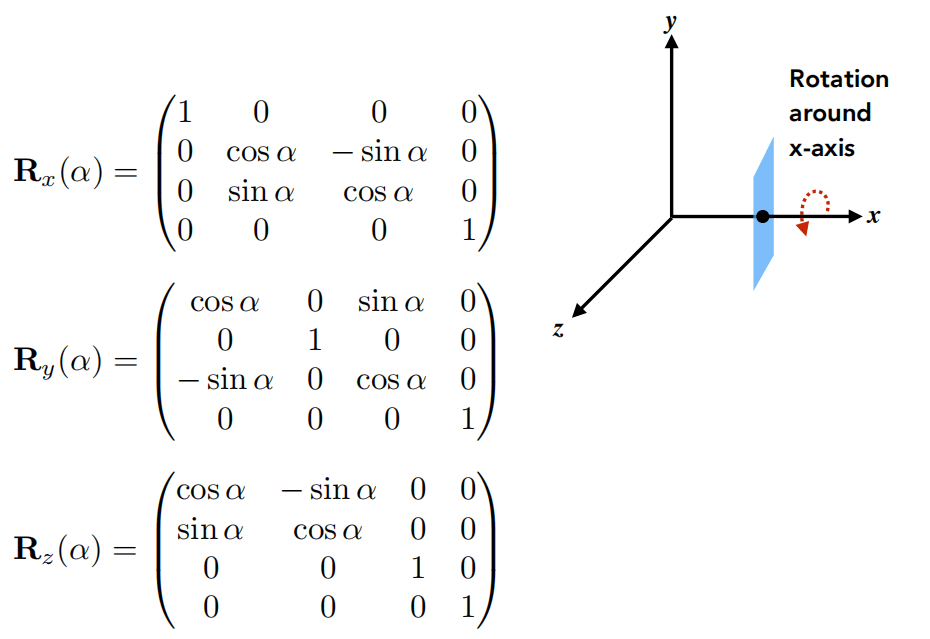
使用4x4矩阵转换坐标系示例

炮塔发射一条射线射中物体后，在物体击中位置的法线方向放置一组盒子形状的顶点。

public void testFunction()
{
    if(Physics.Raycast(headPos,transform.forward,out RaycastHit hit))
    {
        Vector3 hitPos = hit.point;
        Vector3 up = hit.normal;
        Vector3 right = Vector3.Cross(up,lookDir).normalized;
        Vector3 forward = Vector3.Cross(right,up);

        Quaternion turretRot = Quaternion.LookRotation(forward,up);
        Matrix4x4 turretToWorld = Matrix4x4.TRS(hitPos,turretRot,Vector3.one);
        Matrix4x4 worldToTurret = turretToWorld.inverse;//逆矩阵

        // 测试用盒子形状顶点数据
        Vector3[] pts = new Vector3[] {
            new Vector3(1,0,1),
            new Vector3(-1,0,1),
            new Vector3(-1,0,-1),
            new Vector3(1,0,-1),
            new Vector3(1,2,1),
            new Vector3(-1,2,1),
            new Vector3(-1,2,-1),
            new Vector3(1,2,-1)
        }
        
        Gizmos.color = Color.red;
        for(int i = 0; i < pts.Length;i++)
        {
            // 把顶点局部坐标转换成基于击中位置的世界坐标
            Vector3 worldPt = turretToWorld.MultiplyPoint3x4(pts[i]);
            Gizmos.DrawSphere(worldPt,0.075f);
        }
    }
}

平移旋转缩放矩阵

mat4 setScale( float x, float y, float z )
{
    return mat4( x, 0.0, 0.0, 0.0,
                 0.0, y, 0.0, 0.0,
                 0.0, 0.0, z, 0.0,
                 0.0, 0.0, 0.0, 1.0 );
}

mat4 setRotation( float x, float y, float z )
{
    float a = sin(x); float b = cos(x); 
    float c = sin(y); float d = cos(y); 
    float e = sin(z); float f = cos(z); 

    float ac = a*c;
    float bc = b*c;

    return mat4( d*f,      d*e,       -c, 0.0,
                 ac*f-b*e, ac*e+b*f, a*d, 0.0,
                 bc*f+a*e, bc*e-a*f, b*d, 0.0,
                 0.0,      0.0,      0.0, 1.0 );
}

mat4 setTranslation( float x, float y, float z )
{
    return mat4( 1.0, 0.0, 0.0, 0.0,
                 0.0, 1.0, 0.0, 0.0,
                 0.0, 0.0, 1.0, 0.0,
                 x,     y,   z, 1.0 );
}

// 使用例子
void example()
{
    // 这个变换是先旋转再平移。具体顺序是:
    // 1.先绕X轴旋转-0.2弧度
    // 2.再绕Y轴旋转(20.0 + 0.2iTime)弧度
    // 3.最后绕Z轴旋转0.1弧度
    // 4.最后将旋转后的物体平移到(0.0, -0.5, -5.0)的位置
    mat4 mdv = setTranslation( 0.0, -0.5, -5.0 ) * setRotation( -0.2, 20.0+0.2*iTime, 0.1 );

    vec4 p1 = vec4();
    // 使用矩阵转换坐标系
    vec4 p2 = mdv * p1;
}