大鹏笔记

# 【2D矩阵】

# 数学意义

应用于物体的平移、旋转、缩放、坐标系变换。

# 2D矩阵变换

# 缩放

Markdown 图片

# 旋转

Markdown 图片

// OpenGL里使用矩阵旋转uv示例
vec2 rotate(vec2 uv,float a)
{
    mat2 mat = mat2(cos(a),-sin(a),sin(a),cos(a));
    vec2 uv2 = uv - 0.5;
    vec2 uv3 = mat * uv2;
    return uv3 + 0.5;
}

# 平移

Markdown 图片

# 逆矩阵

逆矩阵可以让变换进行反向操作。

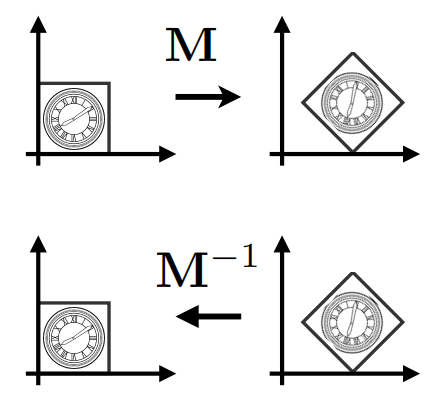
Markdown 图片

# 矩阵合并

可以让移动、旋转等进行合并成一个矩阵，使用合并后的矩阵，能直接让指定向量进行变换。

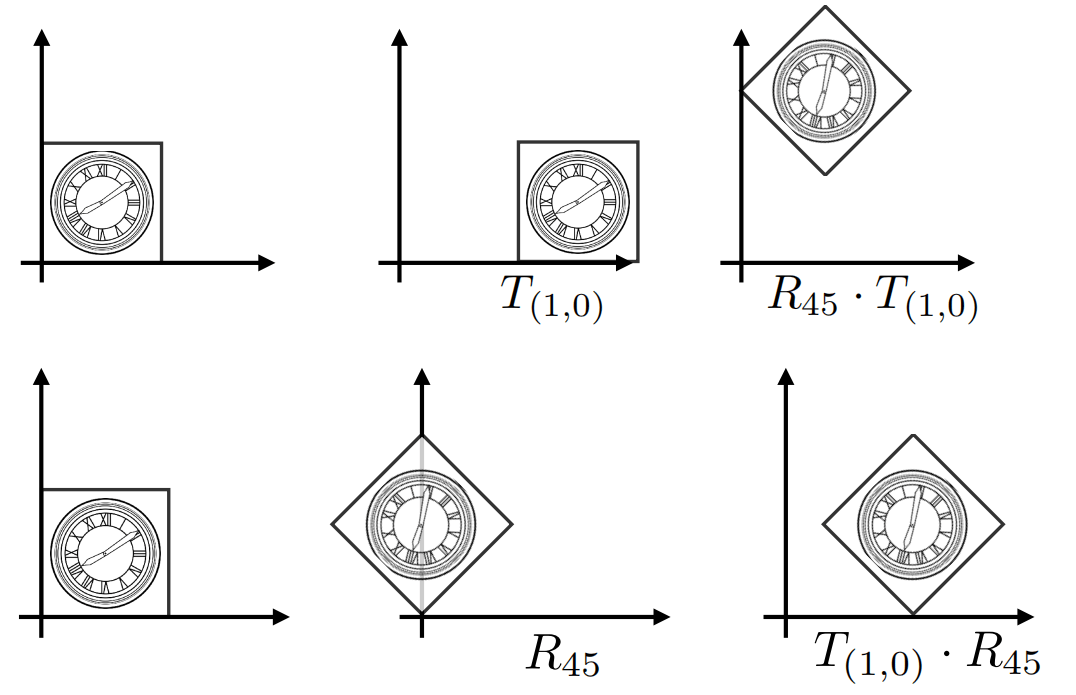
Markdown 图片

观察上面两种不同的矩阵相乘，可以发现，矩阵的乘法不具有交换律。先移动再旋转和先旋转再移动的结果是不一样的。

注意，先移动再旋转，向量乘法里的矩阵顺序是相反的，既 旋转M X 移动M。

# 齐次坐标

2d矩阵是3X3的，增加一个维度是为了处理移动。

Markdown 图片

一个2d数据加一个维度变成3d数据，是有意义的。 其中前面两个是x与y，第三个数据表示该数据是否是点（否则是向量）。 这么理解有个重要的性质：

  • 向量 + 向量 = 向量
  • 点 - 点 = 向量
  • 点 + 向量 = 点
  • 点 + 点 = 两个点之间的中间点

← 【3D矩阵】 →